This is a convenience function for generating scale expansion vectors for the expand argument of scale_(xy)_continuous and scale_(xy)_discrete The expansion vectors are used to add some space between the data and the axesMinimize the functions a) f(x, y) = 1/2(x1) y s t 1xco 2y0 b) f(x1, x2) = (x14)2 (x2 4)2 s t X1 X2 2 = 0 using any penalty function method Illustrate the performance index (minimizing function), constraint function and solution point graphicallyBinomial Theorem – Explanation & Examples A polynomial is an algebraic expression made up of two or more terms which are subtracted, added or multiplied A polynomial can contain coefficients, variables, exponents, constants and operators such addition and subtraction There are three types of polynomials, namely monomial, binomial and trinomial A monomial is an algebraic
The Binomial Theorem 1 Objectives Pascal S Triangle Coefficient Of X Y N When N Is Large Notation Ncrncr Ppt Download
(x+y)^1/2 expand
(x+y)^1/2 expand-Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepBTW, both itertoolsimap and Python3's map will accept the following itertoolsimap(lambda x,y xy, itertoolsrepeat(x), y) The default Python2's map will not stop at the end of y and will insert Nones


What Is The Binomial Expansion For 1 X 1 Quora
In the previous section you learned that the product A(2x y) expands to A(2x) A(y) Now consider the product (3x z)(2x y) Since (3x z) is in parentheses, we can treat it as a single factor and expand (3x z)(2x y) in the same manner as A(2x y) This gives us If we now expand each of these terms, we haveThe special cases α = 1 / 2 and Here we employ a method called "indirect expansion" to expand the given function This method uses the known Taylor expansion of the exponential function In order to expand (1 x)e x as a Taylor series in x,Study the best way to multiply out a rational expression the numerator of the rational expression is log(x^3 15*x^2 75*x 125) The denominator of the rational expression is x^3 3*x 2
Answer Save 5 Answers Relevance Anonymous 1 decade ago Favourite answer use the foil methol (x1)(x2)=x^23x2 (x^23x2)(x3)=x^36x^211x6 2 0Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function Special expansions online The function expand makes it possible to expand a product, itStart with the given expression Expand Remember something like Now let's FOIL the expression Remember, when you FOIL an expression, you follow this procedure
Expand_and_simplify((3x1)(2x4)) The expression in its expanded form and reduced `414*x6*x^2` be returned The online calculator function to expand and collapse an algebraic expression Syntax expand_and_simplify(expression) , expression is the expression to expand Examples expand_and_simplify(`(34)*2`) returns 14This calculator can be used to expand and simplify any polynomial expressionIn the previous section you learned that the product A(2x y) expands to A(2x) A(y) Now consider the product (3x z)(2x y) Since (3x z) is in parentheses, we can treat it as a single factor and expand (3x z)(2x y) in the same manner as A(2x y) This gives us If we now expand each of these terms, we have



Using Binomial Theorem Expand X Y 5 X Y And Hence Find The Value Of Root 2 1 5 Root 2 1 5 Math Binomial Theorem Meritnation Com



I Am Taking A Taylor Series Expansion Of A Function F X I Wish To Expand The Function Around The Value G X Is This Allowable
Expand (x 2 3) 6;Yes Let the point have coordinates (x,x) Now find x, so that distance from (x,x) to (3,5) = 10 We calculate distance between points as follows (x3)² (x5)² = 10² (x² 6x 9) (x² 10x 25) = 100 2x² 16x 34 = 100 2x² 16x 66 = 0 Solve for x 2x² 16x 66 = 0 → divide both sides by 2 x² 8x 33 = 0 → factor (x 11) (x 3) = 0 x = 11 or 3 So points (11, 11We begin by witting the extended binomial theorem



The Coefficients Of X 2y 2 Yzt 2 And Xyzt In The Expansion Of X Y Z T 4 Are In The Ratio A 4 2 1 B 1 2 4 C 2 4 1 D 1 4 2 Math Binomial Theorem Meritnation Com



Expand X 1 2y 1 3z 2 Brainly In
Answer Save 5 Answers Relevance Anonymous 1 decade ago Favourite answer use the foil methol (x1)(x2)=x^23x2 (x^23x2)(x3)=x^36x^211x6 2 0Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyEq1= Expand(1 x^2)^5 eq1 // Factor Factoreq1,GaussianIntegers>True OptionsFactor eq1= Expand(x1)^5 (y1)^2 , y eq1 Simplify Sqrt @H abcdCos @ Θ DL ^2 D Simplify Simplify @ Sqrt @H abcdCos @ Θ DL ^2 D, 8 a > 0, b ˛ Reals, c ˛ Complexes, Π 2 < Θ < Π


The Binomial Theorem 1 Objectives Pascal S Triangle Coefficient Of X Y N When N Is Large Notation Ncrncr Ppt Download



How Do You Expand The Binomial X Y 5 Socratic
\begin{aligned} 4(xy) x(x2) &= 4x 4y x^2 2x \\ &= x^2 6x 4y\ _\square \end{aligned} 4 (x y) x (x 2) = 4 x 4 y x 2 2 x = x 2 6 x 4 y 95 97 99 101 What is the coefficient of x x x after you simplify the expressionTo see this rule, we just expand out what the exponents mean Let's start out with a couple simple examples \begin{align*} 3^4 3^2 &= (3 \times 3 \times 3 \times 3) \times (3 \times 3)\\ &= 3 \times 3 \times 3 \times 3 \times 3 \times 3\\ &= 3^6 \end{align*} \begin{align*} y^2 y^3 &= (y \times y) \times (y \times y \times y)\\ &= y \times yPrecalculus The Binomial Theorem The Binomial Theorem 1 Answer



Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download



Using The Binomial Theorem College Algebra
To see this rule, we just expand out what the exponents mean Let's start out with a couple simple examples \begin{align*} 3^4 3^2 &= (3 \times 3 \times 3 \times 3) \times (3 \times 3)\\ &= 3 \times 3 \times 3 \times 3 \times 3 \times 3\\ &= 3^6 \end{align*} \begin{align*} y^2 y^3 &= (y \times y) \times (y \times y \times y)\\ &= y \times yFree expand & simplify calculator Expand and simplify equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyThis is a similar answer to Artem Lenskiy's answer to What is the binomial expansion of math(1x) ^{2}/math?



If X Y 1 Then R 0 N R Ncrx Ry N R Equals


Wtamu Math Tutorials And Help
Students trying to do this expansion in their heads tend to mess up the powers But this isn't the time to worry about that square on the xI need to start my answer by plugging the terms and power into the TheoremThe first term in the binomial is "x 2", the second term in "3", and the power n is 6, so, counting from 0 to 6, the Binomial Theorem gives me\begin{aligned} 4(xy) x(x2) &= 4x 4y x^2 2x \\ &= x^2 6x 4y\ _\square \end{aligned} 4 (x y) x (x 2) = 4 x 4 y x 2 2 x = x 2 6 x 4 y 95 97 99 101 What is the coefficient of x x x after you simplify the expressionIn elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer depending



General And Middle Term Binomial Theorem Formula Videos Examples



Distributing Expressions Solutions Examples Worksheets Videos Lesson Plans
ExampleIn this example, we find the second order Taylor expansion of f(x,y) = p 1 4x2 y2 about (x0,y0) = (1,2) and use it to compute approximately f(11,5)We first compute all partial derivatives up to order 2 at (x0,y0) f(x,y) =How do you expand (x1)(x2)(x3)?This can then be written as (x^2 2xy y^2)(x^2 2xy y^2) and expand that out now to be 1x^4 (2xy)(x^2) x^2y^2 (2xy)(x^2) 4x^2y^2 (2xy)(y^2) (y^2)(x^2) (y^2)(2xy) 1y^4


Print Tolerance Tuning Horizontal Xy Expansion Duet3d



Binomial Theorem Wikipedia
F = x y z = x (y z) AND (multiply) has a higher precedence than OR (add) = (x y) (x z) use distributive law to change to product of OR terms = (x y z z') (x y y' z) expand 1st term by ORing it with z z', and 2nd term with y y' = (x y z) (x y z') (x y z) (x y' z) = M0 • M1 • M2 = Π(0, 1, 2) product of 0Y xTy st jjyjj 2 1 CauchySchwarz implies that xTy jjxjjjjyjj jjxjj and y= x jjxjj achieves this bound Proof of (3) We have jjxjj 1 =max y xTy st jjyjj 1 1 So y opt= sign(x) and the optimal value is jjxjj 1 2 Positive semide nite matrices We denote by S n the set of all symmetric (real) n nmatrices 21 De nition De nition 6 A matrixY to the sixth power Times six squared so times six squared times X to the third squared which that's X to the 3 times 2 or X to the sixth and so this is going to be equal to Let's see it's going to be 10 times 27 times 36 times 36 and then we have, of course, our X to the sixth and Y to the sixth
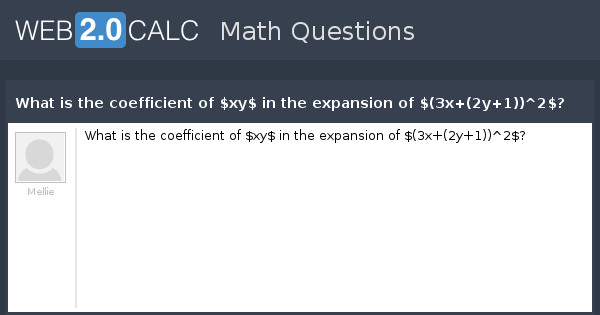


View Question What Is The Coefficient Of Xy In The Expansion Of 3x 2y 1 2
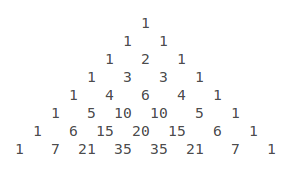


How Do You Find The Binomial Expansion Of X Y 7 Socratic
Expansions Which Have LogarithmBased Equivalents Summantion Expansion Equivalent Value Comments x nFind an answer to your question expand by using identity (2x y z)^2 10 The mean height of boys of a class is 150 cm When a boy leaves the class, the meanheight comes down by 05 cm Find the height of the boyAnswThe main formula is Now put n=1/2 and then solve you will get this Click on Upvote if you like my simple and short explanation
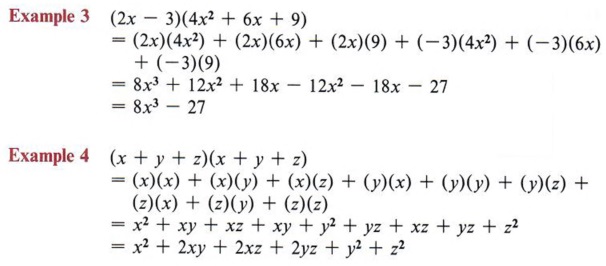


Expand Terms Multiply Polynomials With Step By Step Math Problem Solver
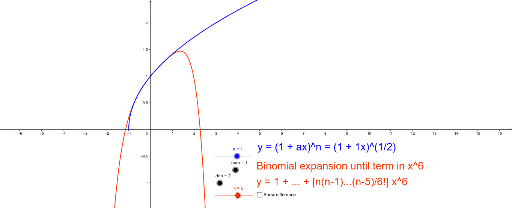


Binomial Expansion Geogebra
Expand the trigonometric expression cos(x y)Simplify the cos function input x y to x or y by applying standard identitiesHow do you use the binomial series to expand #(1x)^(1/2)#?Answer Save 5 Answers Relevance Anonymous 1 decade ago Favourite answer use the foil methol (x1)(x2)=x^23x2 (x^23x2)(x3)=x^36x^211x6 2 0



Expand Using Identity 3 X Minus 2 Y Z Whole Square Brainly In



What Is The Expansion Of Math 1 X 1 Math Quora
Y xTy st jjyjj 2 1 CauchySchwarz implies that xTy jjxjjjjyjj jjxjj and y= x jjxjj achieves this bound Proof of (3) We have jjxjj 1 =max y xTy st jjyjj 1 1 So y opt= sign(x) and the optimal value is jjxjj 1 2 Positive semide nite matrices We denote by S n the set of all symmetric (real) n nmatrices 21 De nition De nition 6 A matrixTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x(1y^2)dxy(1x^2) dy=0`The special cases α = 1 / 2 and Here we employ a method called "indirect expansion" to expand the given function This method uses the known Taylor expansion of the exponential function In order to expand (1 x)e x as a Taylor series in x,



Answered In The Third Order Taylor Expansion Of Bartleby
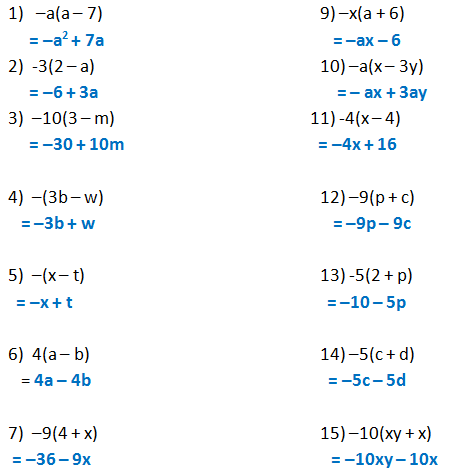


Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreBTW, both itertoolsimap and Python3's map will accept the following itertoolsimap(lambda x,y xy, itertoolsrepeat(x), y) The default Python2's map will not stop at the end of y and will insert Nones≈ f(x0,y0) fx(x0,y0)∆x fy(x0,y0)∆y 1 2 fxx(x0,y0)∆x 2 2f xy(x0,y0)∆x∆yfyy(x0,y0)∆y 2 = 3 4 3∆x 2 3∆y 10 27∆x 2 − 8 27∆x∆y 5 54∆y 2 In particular, with ∆x= 01 and ∆y= 005, f(11,5) ≈ 3 4 3(01) 2 3(005) 10 27(001)− 8 27(0005) 5 54() = The actual value, to four decimal



Logarithm Rules Video Lessons Examples And Solutions


Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community
Math 408, Actuarial Statistics I AJ Hildebrand Variance, covariance, and momentgenerating functions Practice problems — Solutions 1 Suppose that the cost of maintaining a car is given by a random variable, X, with meanChoose variable to solve for SolveWhile positive integer powers of 1 x 1x 1 x can be expanded into polynomials (\big((eg (1 x) 3 = 1 3 x 3 x 2 x 3), (1x)^3 = 13x3x^2x^3\big), (1 x) 3 = 1 3 x 3 x 2 x 3), this does not make f (x) f(x) f (x) a polynomial, so there cannot be a finite sum of monomial terms that equals f (x) f(x) f (x) But there is a way



I Am Taking A Taylor Series Expansion Of A Function F X I Wish To Expand The Function Around The Value G X Is This Allowable



Binomial Theorem Wikipedia
Question How do you simplify (x7)^2 Answer by jim_thompson5910() (Show Source) You can put this solution on YOUR website!Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepBest solutions with stepbystep explanations and reasoning tips



Pdf High Temperature Expansion Of The Free Energy In The Two Dimensional Xy Model



The Coefficients Corresponding To K 0 1 2 4 In The Expansion Of X Y 4 Are Brainly Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyExercise 25 Polynomials Chapter 2 NCERT solution Class 8 NCERT text and video solutions that you will not find anywhere else!Expand the trigonometric expression cos(x y)Simplify the cos function input x y to x or y by applying standard identities
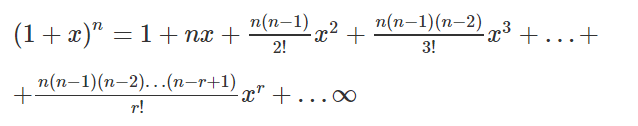


Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



If X Y 1 Then R 0 N R Ncrx Ry N R Equals
This is true of the "difference of squares" you sent us, x 2 y 2 Once you think you know the factors you can check by multiplication Here are three possibilities for factorizations of x 2 y 2 (x y)(x y) (x y)(x y) (x y)(x y) Expand each of them and see which simplifies to x 2 y 2 PennyMinimize the functions a) f(x, y) = 1/2(x1) y s t 1xco 2y0 b) f(x1, x2) = (x14)2 (x2 4)2 s t X1 X2 2 = 0 using any penalty function method Illustrate the performance index (minimizing function), constraint function and solution point graphicallyChoose variable to solve for Solve



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



Simplify The Expression Ppt Video Online Download
Expansions Which Have LogarithmBased Equivalents Summantion Expansion Equivalent Value Comments x nExpand (x1)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Move to the left ofSOLUTION 13 Begin with x 2 xy y 2 = 1 Differentiate both sides of the equation, getting D ( x 2 xy y 2) = D ( 1 ) , 2x ( xy' (1)y) 2 y y' = 0 , so that (Now solve for y' ) xy' 2 y y' = 2x y, (Factor out y' ) y' x 2y = 2 x y, and the first derivative as a function of x and y is (Equation 1)



Pokemon Tcg Xy Furious Fists Expansion Pocketmonsters Net



Solved Find The Coefficient Of X 2y 3z 3 In The Expansion Chegg Com
Subject to the condition x < 1, Binomial theorem for a rational index is (1x)^n = 1 nx {n(n1)/1(2)}x^2 {n(n1)(n2/1(2)(3)}x^3 to infinity=1 (1/2)x (3/8)x^2 (5/16) x^3 In the binomial expansion formula for (1x)^n = 1 nx (n(n1))/(2!)x^2 substitute x for x and 1/2 for n The resultExpand (xy)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Multiply by Add and



Differential Equations Solved Examples Find The First 6 Non Zero Terms Of The Power Series Expansion About X 0 For A General Solution To The Given Differential Equation Y X 2y Xy 0
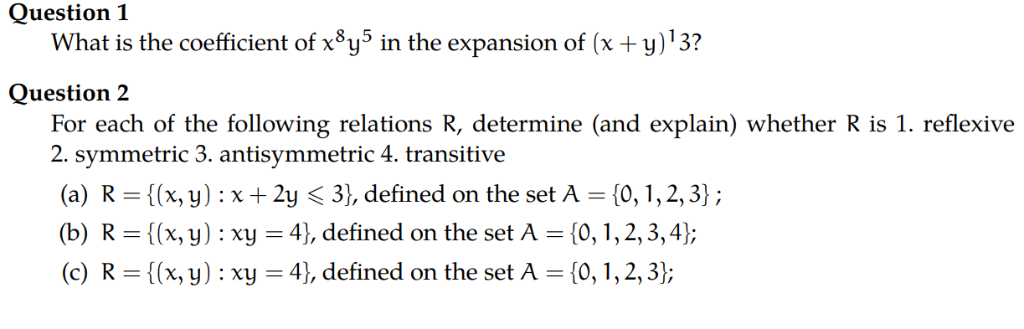


Solved Question 1 What Is The Coefficient Of X8y5 In The Chegg Com
Y ≥ x}, which is the region above the line y = x;This yields a triangle whose leftmost xvalue is 0 and whose rightmost xvalue is 1/2 (which is only seen by drawing the figure!) See figure above, right To compute the probability, we double integrate the joint density over this subset of the support set P(Y ≥ X) = Z 1/2 0 Z 1−x xThis calculator can be used to expand and simplify any polynomial expression



Jacobians New


Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community
An outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for theirHow do you expand (x1)(x2)(x3)?Minimize the functions a) f(x, y) = 1/2(x1) y s t 1xco 2y0 b) f(x1, x2) = (x14)2 (x2 4)2 s t X1 X2 2 = 0 using any penalty function method Illustrate the performance index (minimizing function), constraint function and solution point graphically
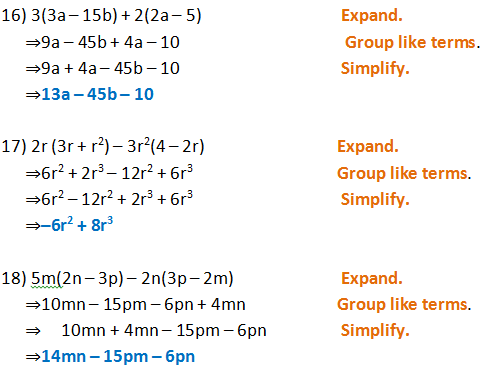


Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths
How do you expand (x1)(x2)(x3)?Get the answer to Expand (x1)^2 with the Cymath math problem solver a free math equation solver and math solving app for calculus and algebraImport numpy as np x = nparray((1,2,3,4)) print 'Array x' print x print '\n' y = npexpand_dims(x, axis = 0) print 'Array y' print y print '\n' print 'The shape of X and Y array' print xshape, yshape print '\n' # insert axis at position 1 y = npexpand_dims(x, axis = 1) print 'Array Y after inserting axis at position 1' print y print '\n' print 'xndim and yndim' print xndim,y



Expand 1 X Y 3 3 Class 9
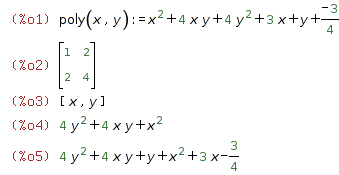


Wxmaxima Html Export
Learn about expand using our free math solver with stepbystep solutions



Binomial Theorem Wikipedia



The Binomial Theorem



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



Jacobians New



Binaomial Expansion Nov 27 09


What Is The Expansion Of Math 1 X 1 Math Quora



Pascal S Triangle A Great Number Triangle Whose Entries Are Coefficients Of A Binomial Expansion Math Methods Studying Math Mathematics
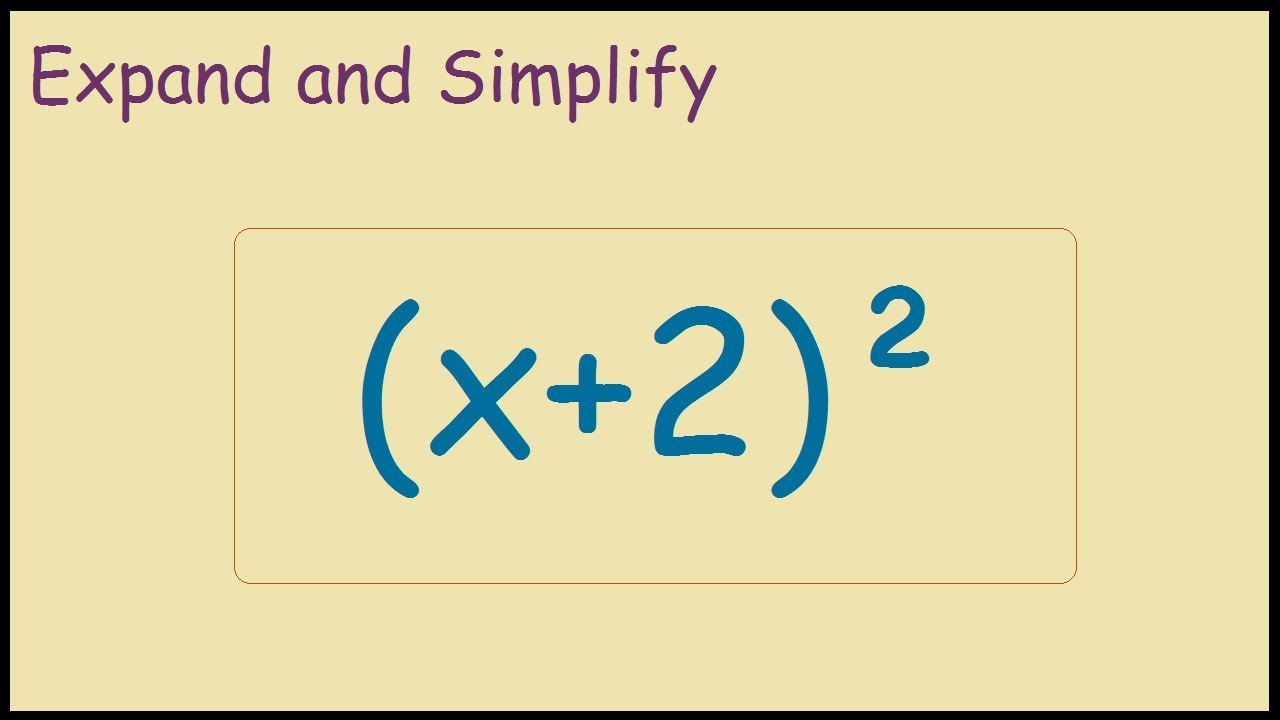


X 2 2 Expand And Simplify Using Foil Method Youtube



Expanding Binomials W O Pascal S Triangle Video Khan Academy



Sketch A Diagram And Expand The Polynomial Geometrically X 3y 2z 2



Solved Question 1 1 What Is The Coefficient Of Roy2 In T Chegg Com
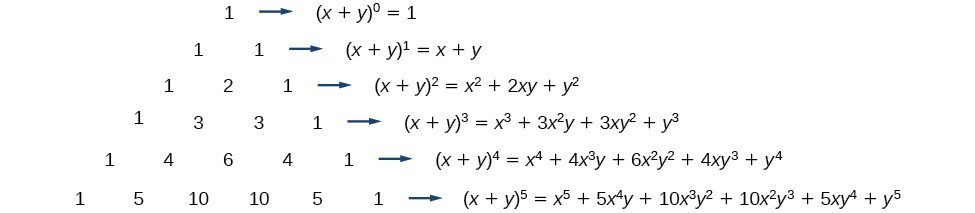


Using The Binomial Theorem College Algebra



Expanding Brackets Worksheet Page 1 Line 17qq Com



The Binomial Theorem Fractional Powers Expanding 1 2x 1 3 Youtube



Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube


4 The Binomial Theorem



Ib Hl Math Homework 2 Logs Binomial Theorem And Induction
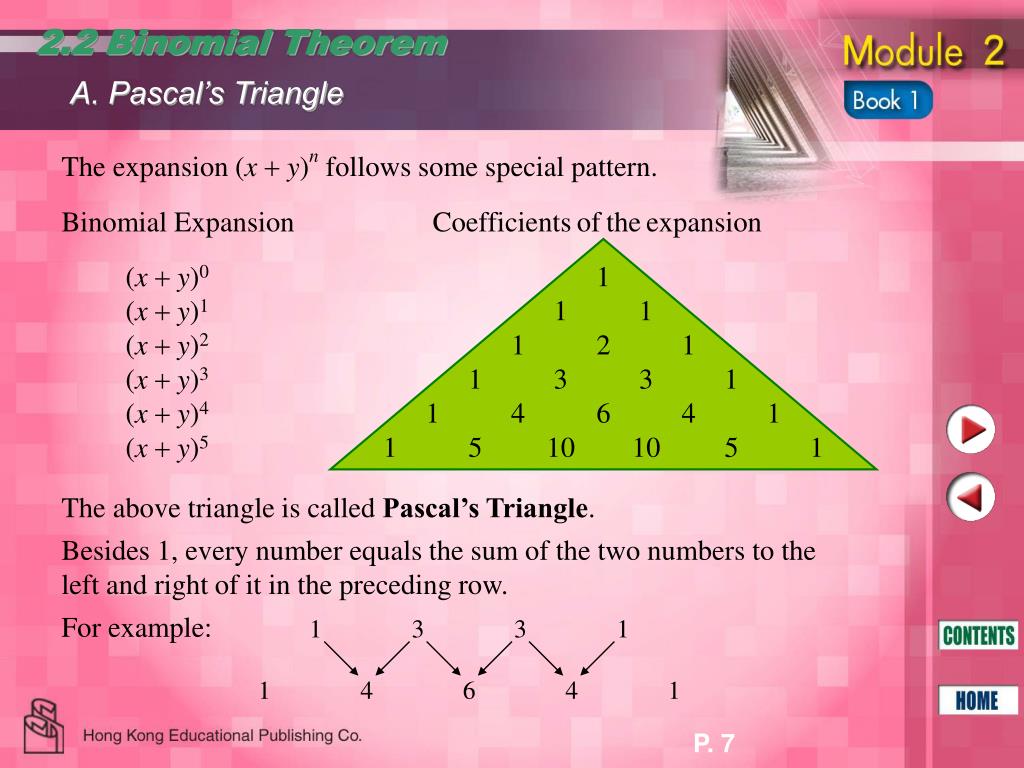


Ppt Binomial Theorem Powerpoint Presentation Free Download Id 403


What Is The Binomial Expansion For 1 X 1 Quora



Solved Expand The Following Functions About The Point Xo Chegg Com


Expand E X Cosy By Taylors S Theorem About The Point 1 P 4 Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community


The Number Of Terms In The Expansion Of X Y Z N Studyrankersonline



Can Someone Help Me With This Problem On 2c Step By Step It S Saids Simplify Without Negatives Algebra



9 5 The Binomial Theorem


What Is The Binomial Expansion Of Math 1 X 2 Math Quora



The Coefficients Corresponding To K 0 1 2 4 In The Expansion Of X Y 4 Are A 1 4 6 6 4 1 B 0 4 6 4 0 C 0 1 4 6 4 1 0 D 1 4 6 4 1 Not A Studydaddy Com



Binomial Expansion Made Easy Expand X Y Algebra Youtube



Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5



The Binomial Theorem 1 Objectives Pascal S Triangle Coefficient Of X Y N When N Is Large Notation Ncrncr Ppt Download



Solved Consider The Function G X H E X H H 1 2 Chegg Com



Solved Use The Binomial Series To Expand The Function As Chegg Com



Ex 2 5 4 Expand Each Of The Following Using Suitable



How Can We Expand X Y 1 2 Youtube



Conic Section From Expanded Equation Circle Parabola Video Khan Academy



Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9



Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9



Using The Binomial Theorem College Algebra



Solved Use The Binomial Series To Expand The Function As Chegg Com


Expand E X Log 1 Y By Maclaurin S Theorem Up To The Third Degree Term Sarthaks Econnect Largest Online Education Community


Expand 1 X Y 3 Whole Cube Studyrankersonline



Section 8 5 The Binomial Theorem Ppt Download



In The Expansion Of 1 X X 3 X 4 10 The Coefficient Of X 4
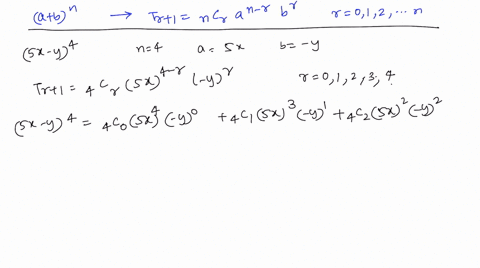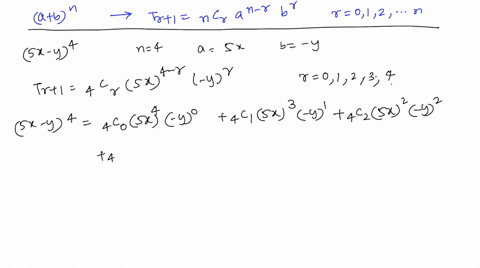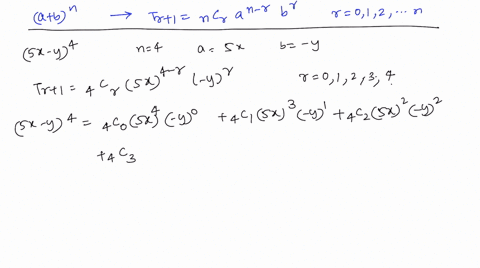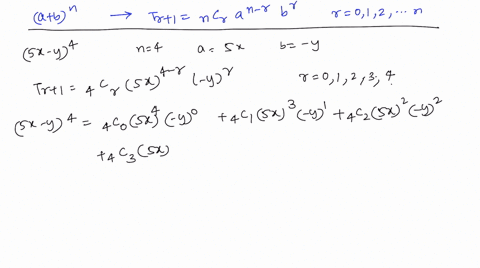


Solved Use The Binomial Theorem To Expand And Sim



Expanding Brackets Worksheets Common Core Worksheets
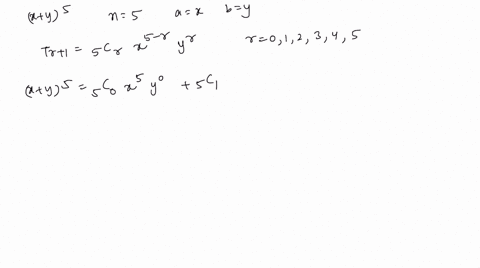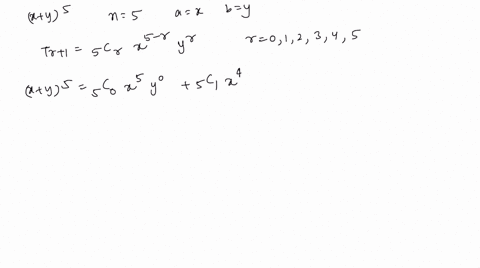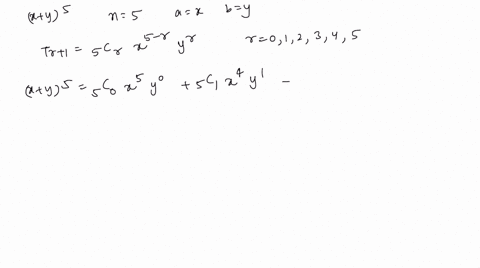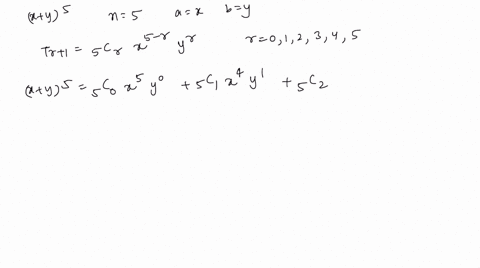


Solved Use The Binomial Theorem To Expand And Sim



Alg2 March28 The Answers



Pascal S Triangle And The Coefficients In The Expansion Of Binomials Ck 12 Foundation



Expand And Simplify Binomial Squares 2x 3y 2 Youtube


What Is The Binomial Expansion Of Math 1 X 2 Math Quora



No comments:
Post a Comment